Lemme de Scheffi - Math'φsics

Lemme de Scheffi

Formulaire de report
Problème d'affichage Contenu de la note peu pertinent
Lemme de Scheffi :
\(\forall n,X_n\geqslant0\)

\(X_n\) converge en probabilité vers \(X\)

\(\forall n,{\Bbb E}[X_n]\lt +\infty\)

\({\Bbb E}[X]\lt +\infty\)

$$\Huge\iff$$

$${\Bbb E}[X_n]{\underset{n\to+\infty}\longrightarrow}{\Bbb E}[X]\implies X_n\overset{L^1}{\underset{n\to+\infty}\longrightarrow} X$$
(Convergence Lp de variables aléatoires)

Démonstration du lemme de Scheffi :

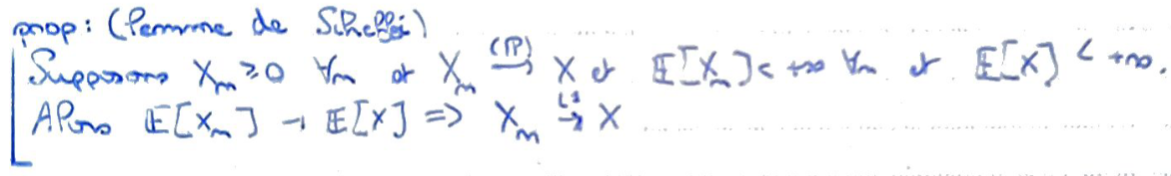
On veut majorer la norme \(L^1\) de la différence. Pour cela, on décompose \(\lvert X_n-X\rvert\) selon le signe de \(X_n-X\).

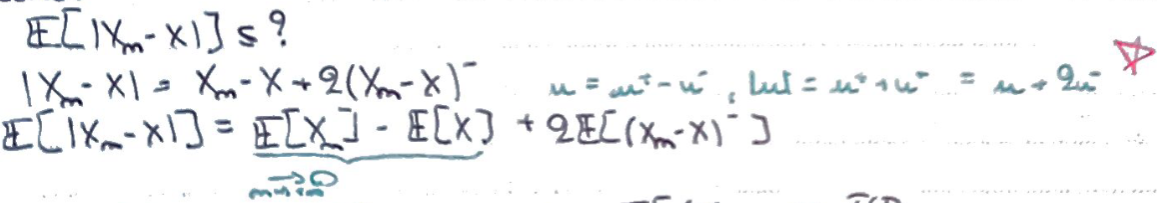
On peut utiliser le TCD pour conclure, en utilisant le fait que \(X_n\geqslant0\) (hypothèse).
Rétroliens :
- Convergence en probabilité